Available with Image Server
Una de las claves de la derivación de características hidrológicas de una superficie es la capacidad de determinar la dirección de flujo desde cada celda en el ráster. Se hace con la herramienta Dirección de flujo.
Esta herramienta toma una superficie como entrada y proporciona como salida un ráster que muestra la dirección del flujo que sale de cada celda. Si se elige la opción Ráster de caída de salida, se crea un ráster que muestra una proporción del cambio máximo en la elevación desde cada celda a lo largo de la dirección del flujo hasta la longitud de la ruta entre los centros de celda y se expresa en porcentajes. Si se elige la opción Forzar todas las celdas de eje para que se desplacen hacia fuera, todas las celdas del borde del ráster de superficie fluirán hacia fuera del ráster de superficie.
Existen ocho direcciones de salida válidas que se relacionan con las ocho celdas adyacentes hacia donde puede ir el flujo. Este enfoque comúnmente se denomina el modelo de flujo de ocho direcciones (D8) y sigue un acercamiento presentado en Jenson and Domingue (1988).
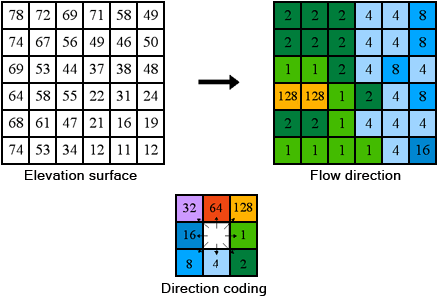
Calcular la dirección del flujo utilizando el método D8
En el método D8, la dirección del flujo está determinada por la dirección del descenso más pronunciado, o caída máxima, desde cada celda (Jenson y Domingue, 1988). Se calcula de la siguiente manera:
caída_máxima = cambio_en_valor_z/distanciaLa distancia se calcula entre los centros de las celdas. Por ejemplo, si el tamaño de celda es 1, la distancia entre dos celdas ortogonales es 1, y la distancia entre dos celdas diagonales es la raíz cuadrada de 2. Si el descenso máximo de varias celdas es el mismo, la vecindad se agranda hasta que se encuentra el descenso más empinado.
Cuando se encuentra la dirección de un descenso más empinado, la celda de salida se codifica con el valor que representa esa dirección.
Si todos los elementos próximos son más altos que la celda de procesamiento, se considerará un ruido que se rellena con el valor más bajo de los elementos próximos, y tiene una dirección de flujo hacia esta celda. Sin embargo, si un sumidero de una celda está junto al borde físico del ráster o tiene como mínimo una celda NoData como vecino, no se rellena porque la información del vecino no es suficiente. Para que se considere como un sumidero verdadero de una celda, debe estar presente toda la información de vecino.
Si dos celdas fluyen entre sí, se trata de sumideros que tienen una dirección de flujo indefinida. Este método que deriva una dirección de flujo de un modelo digital de elevación (DEM) se presenta en Jenson and Domingue (1988).
Las celdas que son sumideros se pueden identificar utilizando la herramienta Sumidero. Para obtener una representación precisa de la dirección de flujo en una superficie, rellene los sumideros antes de usar la herramienta Dirección del flujo.
Calcular la dirección del flujo utilizando el método MFD
En el método MFD, el flujo se divide entre todos los vecinos de pendiente descendente (Qin et al., 2007). La cantidad de flujo que recibe cada vecino pendiente abajo se estima en función del gradiente máximo de la pendiente, lo que permite las condiciones locales del terreno. La expresión para estimar la MFD es la siguiente:
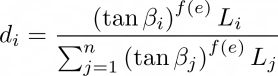
Dónde:
- di = Porción de flujo de cada celda que fluye hacia la celda i
- f (e) = Exponente que se adapta a las condiciones locales del terreno y viene dado por
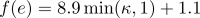
- β = Ángulo de pendiente descendente (en radianes)
- n = número de celdas que fluyen hacia la celda i
- Li, Lj = Factor ajustado para tener en cuenta la distancia entre la celda de procesamiento y las celdas ortogonales y diagonales
- κ = Caída máxima en las celdas que fluyen hacia la celda i
Referencias
Jenson, S. K., and Domingue, J. O. 1988. "Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis". Photogrammetric Engineering and Remote Sensing 54 (11): 1593-1600.
Qin, C., Zhu, A. X., Pei, T., Li, B., Zhou, C., & Yang, L. 2007. "An adaptive approach to selecting a flow partition exponent for a multiple flow direction algorithm." International Journal of Geographical Information Science 21(4): 443-458.