Available with Image Server
La herramienta Parámetros de superficie determina los parámetros de una superficie ráster, como la orientación, la pendiente y la curvatura.
Orientación
El parámetro de superficie Orientación identifica la dirección de la pendiente descendente. El valor de cada celda del ráster de salida indica la dirección de brújula a la que apunta la superficie en esa ubicación. Se mide en el sentido de las agujas del reloj en grados de 0 (hacia el norte) a 360 (hacia el norte, nuevamente), formando un círculo completo. Las áreas planas que no tienen dirección de pendiente descendente tienen un valor de -1.
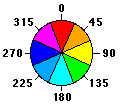
En las imágenes siguientes se muestra un dataset de elevación de entrada y el ráster de orientación de salida.
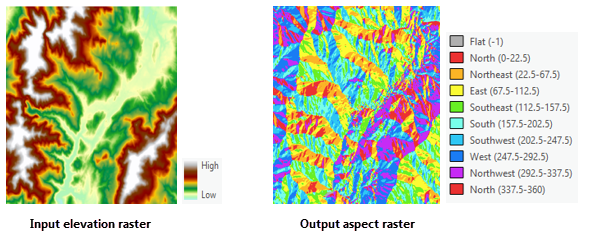
Aplicaciones de orientación
Con el tipo de parámetro de superficie Orientación, puede hacer lo siguiente:
- Buscar todas las pendientes mirando al norte en una montaña, como parte de una búsqueda de las mejores pendientes para hacer esquí.
- Calcular la iluminación solar para cada ubicación de una región como parte de un estudio para determinar la diversidad de vida en cada sitio.
- Buscar todas las pendientes hacia el sur en una región montañosa para identificar las ubicaciones donde es posible que la nieve se derrita primero, como parte de un estudio para identificar las ubicaciones residenciales que son propensas a ser afectadas primero por la escorrentía.
Cálculos de orientación geodésica
La orientación geodésica en una ubicación es la dirección angular de la pendiente descendente respecto al norte, medida en un plano tangente a la superficie del elipsoide (el plano azul en la ilustración que aparece a continuación).
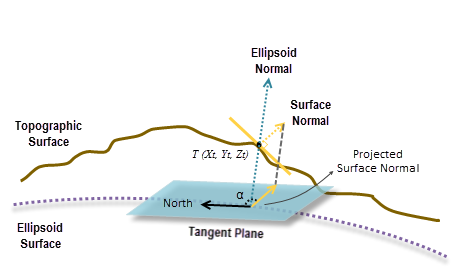
Para calcular la orientación en cada ubicación, se ajusta una superficie cuadrática o bicuadrática a las celdas vecinas con el método por mínimos cuadrados (LSM). Se calcula una normal a la superficie en la ubicación de la celda de esa superficie. En la misma ubicación, también se calcula una normal a la elipsoide en perpendicular al plano tangente de la superficie de elipsoide.
Dado que el plano tangente de la superficie elipsoide se considera el plano de referencia, la normal a la superficie se proyecta en el plano. Finalmente, se calcula la orientación geodésica midiendo el ángulo α en el sentido de las agujas del reloj entre el norte y la proyección de la normal a la superficie (consulte la ilustración de arriba).
Pendiente
El parámetro de superficie Pendiente identifica la inclinación en cada celda de una superficie de ráster. Mientras menor sea el valor de la pendiente, más plano será el terreno; mientras más alto sea el valor de la pendiente, más empinado será el terreno.
El ráster de pendiente de salida se puede calcular en uno de dos tipos de unidades posibles: grados o porcentaje (elevación en porcentaje). La elevación en porcentaje se comprende mejor si se considera como la elevación dividida entre el avance, multiplicada por 100. Considere el triángulo B más abajo. Cuando el ángulo es de 45 grados, la elevación es igual al avance, y la elevación en porcentaje es 100%. A medida que la pendiente alcanza la vertical (90 grados), como se puede ver en el triángulo C, la elevación en porcentaje comienza a acercarse al infinito.
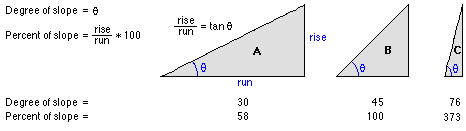
Pendiente se ejecuta con más frecuencia en un dataset de elevación, tal y como se muestra en las siguientes imágenes. Las pendientes más empinadas están sombreadas en marrón más oscuro en el ráster de pendiente de salida.
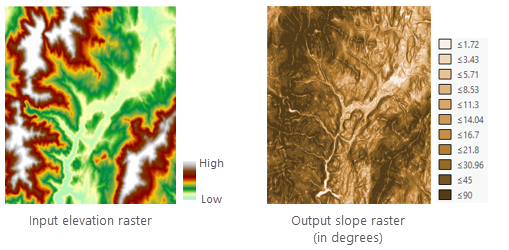
La herramienta también se puede utilizar con otros tipos de datos continuos, como la población, para identificar cambios marcados en el valor.
Cálculos de pendiente geodésica
La pendiente geodésica es el ángulo formado entre la superficie topográfica y la superficie del elipsoide. Toda superficie paralela a la superficie del elipsoide tiene una pendiente de 0. Para calcular la pendiente en cada ubicación, se ajusta una superficie cuadrática o bicuadrática a las celdas vecinas con el método por mínimos cuadrados (LSM). Se calcula una normal a la superficie en la ubicación de la celda de esa superficie. En la misma ubicación, también se calcula una normal a la elipsoide en perpendicular al plano tangente de la superficie de elipsoide. La pendiente, en grados, se calcula desde el ángulo entre la normal a la elipsoide y la normal a la superficie topográfica. Este ángulo es el mismo que el formado entre la superficie topográfica y la superficie del elipsoide.
Vista general de la curvatura de la superficie
La curvatura es una colección de tipos de parámetros de superficie utilizados para describir la forma de una superficie, típicamente a lo largo de una línea en la superficie, creada por la intersección de un plano a través de la superficie. Conceptualmente, la curvatura geométrica encuentra el círculo que mejor se ajusta (círculo oscilante) para aproximarse a la forma de la curva en cualquier punto. La curvatura es la recíproca del radio de ese círculo (1/r). Una línea más recta se ajustará mejor con un círculo más grande y resulta en una curvatura más pequeña, y una línea curva más cerrada se ajustará mejor con un círculo más pequeño y resulta en una curvatura más grande (Crane, 2018).
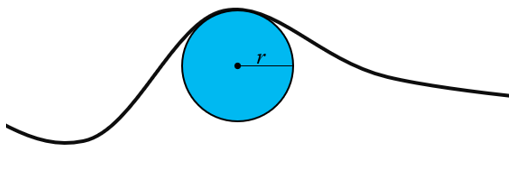
Curvatura de perfil (línea de pendiente normal)
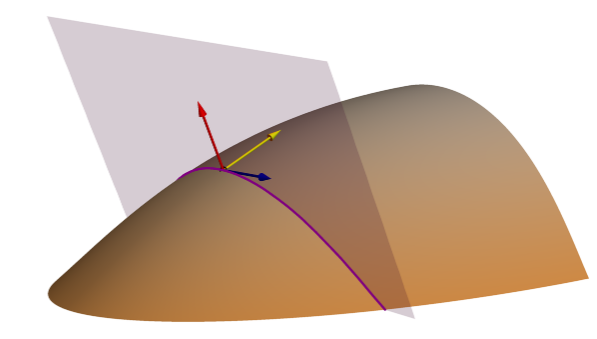
El parámetro de superficie Curvatura de perfil (línea de pendiente normal) mide la curvatura normal geométrica a lo largo de la línea de pendiente. A veces denominada curvatura de perfil, puede visualizarse como la forma de una sección transversal vertical (de perfil) a través de la superficie. Como se ilustra a continuación, el plano vertical atraviesa la superficie a lo largo de la línea naranja; si la separáramos, aparecería como un perfil transversal de la superficie.
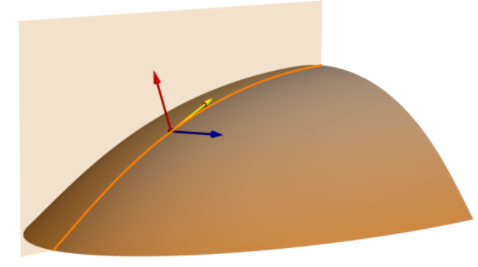
Ese plano se define por dos vectores: la flecha amarilla que muestra la dirección del gradiente o la flecha de la línea de la pendiente, y la flecha roja que indica la normal a la superficie. Es la combinación de estos vectores rojo y amarillo lo que define el plano naranja y su línea de intersección naranja con la superficie. La curvatura del perfil se calcula a lo largo de la línea naranja (línea de pendiente normal) en el plano naranja.
La terminología de la "línea de pendiente normal" de Minár y otros (2020) se utiliza aquí reducir al mínimo la ambigüedad y la confusión con la terminología anterior.
Esta curvatura se suele aplicar para caracterizar la aceleración y deceleración del flujo por la superficie por efecto de la gravedad. A mayor velocidad, el agua puede arrancar y transportar mayores cantidades de material; las zonas de aceleración se convierten en zonas de erosión y las zonas de deceleración en zonas de deposición.
En la imagen siguiente, las áreas de alta curvatura de perfil convexo (línea de pendiente normal) alrededor de la cresta del cono se muestran en morado. Las áreas de alta curvatura de perfil cóncavo (línea de pendiente normal) en la base del cono se muestran en naranja. Las áreas con valores de curvatura pequeños son transparentes.

Los resultados de esta curvatura son diferentes de la salida de la curvatura Perfil de la herramienta Curvatura anterior. Más adelante se explican las diferencias entre la curvatura de perfil y la curvatura (línea de pendiente) de perfil.
La fórmula para calcular la curvatura del perfil (línea de pendiente normal) es la siguiente:
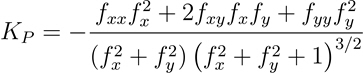
- Donde:
KP = Curvatura (línea de pendiente normal) de perfil
z = f(x,y)
Curvatura tangencial (curva de nivel normal)
El parámetro de superficie Curvatura tangencial (curva de nivel normal) mide la curvatura normal geométrica perpendicular a la línea de pendiente, tangente a la línea de curvas de nivel. Se denomina curvatura tangencial porque mide la curvatura tangente a la línea de curvas de nivel. Se describe como curva de nivel normal (Minár et al., 2020) porque el plano de corte morado que crea la línea morada a lo largo de la cual se calcula la curvatura está definido por el vector de curva de nivel azul y el vector normal de la superficie roja.
La curvatura tangencial (curva de nivel normal) se suele aplicar para caracterizar la convergencia y divergencia topográficas del flujo por la superficie.
En la imagen siguiente, las áreas de alta curvatura tangencial convexa (curva de nivel normal) alrededor de la cresta del cono y la cresta orientada hacia usted se muestran en azul. Se trata de áreas de flujo divergente. Las áreas de alta curvatura tangencial (curva de nivel normal) en el interior del cono muestran flujo convergente en rojo. Las áreas con valores de curvatura pequeños son transparentes.

La fórmula para calcular la curvatura tangencial (curva de nivel normal) es la siguiente:
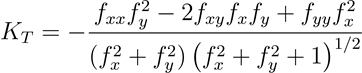
- Donde:
KT = Curvatura (curva de nivel normal) tangencial
z = f(x,y)
Curvatura del plano (curva de nivel proyectada)
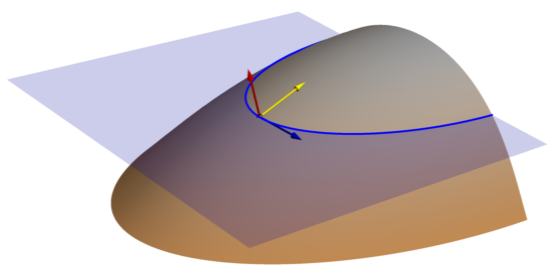
El parámetro de superficie Curvatura del plano (curva de nivel proyectada) mide la curvatura a lo largo de las líneas de curvas de nivel. A veces se denomina curvatura de curvas de nivel y curvatura horizontal. La curvatura de curva de nivel proyectada se mide a lo largo de la línea de curva de nivel en azul, donde el plano horizontal se interseca la superficie.
La fórmula para calcular la curvatura del plano (curva de nivel proyectada) es la siguiente:
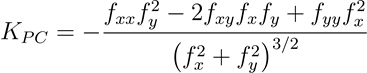
- Donde:
KPC = Curvatura del plano (curva de nivel proyectada)
z = f(x,y)
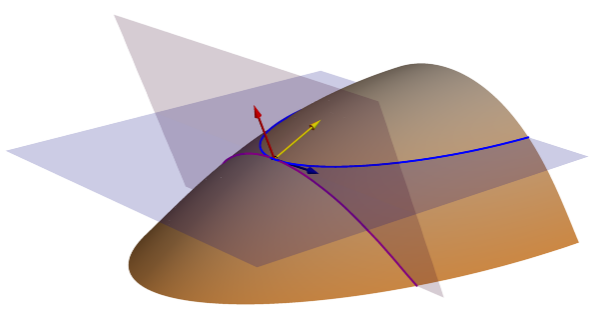
La imagen que aparece a continuación ilustra la diferencia entre la curvatura tangencial (curva de nivel normal), medida a lo largo de la línea morada, y la curvatura del plano (curva de nivel proyectada), medida a lo largo de la línea de curva de nivel azul.
Torsión geodésica de curvas de nivel
El parámetro de superficie Torsión geodésica de curvas de nivel mide la tasa de cambio en el ángulo de pendiente a lo largo de las líneas de curvas de nivel.
La fórmula para calcular la torsión geodésica de curvas de nivel es la siguiente:
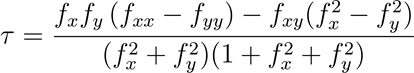
- Donde:
T = Torsión geodésica de curvas de nivel
z = f(x,y)
Curvatura media
El parámetro de superficie Curvatura media mide la curvatura general de la superficie. Se calcula como la media de las curvaturas mínima y máxima. También es matemáticamente equivalente al valor medio de las curvaturas Perfil (línea de pendiente normal) y Tangencial (curva de nivel normal). En la imagen que aparece a continuación se muestra el plano de corte Perfil (línea de pendiente normal) (naranja) y el plano de corte Tangencial (curva de nivel normal) (morado).
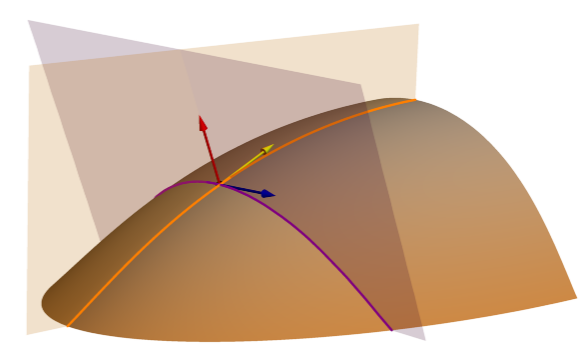
Las curvaturas de perfil (línea de pendiente normal) y tangencial (curva de nivel normal) miden respectivamente la convexidad y la concavidad en una dirección específica; mientras que la curvatura media describe la convexidad o concavidad intrínseca de la superficie, con independencia de la influencia de dirección o gravedad. Su signo (positivo o negativo) no es un indicador definitivo de la convexidad o la concavidad, excepto en valores extremos, dado que una superficie puede ser cóncava en una dirección y, al mismo tiempo, convexa en otra. Unos valores positivos altos indican áreas de denudación máxima, y unos valores negativos altos indican áreas de acumulación máxima (Minár et al., 2020).
La fórmula para calcular la curvatura media es la siguiente:
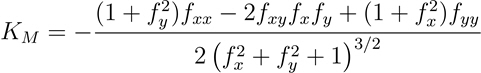
- Donde:
KM = Curvatura media
z = f(x,y)
Curvatura gaussiana
El parámetro de superficie Curvatura gaussiana mide la curvatura general de una superficie. Se calcula como el producto de la curvatura mínima y máxima y puede tomar valores negativos y positivos. Los valores positivos indican que la superficie es convexa en esa celda, y los valores negativos indican que es cóncava. Un valor 0 indica que la superficie es plana.
La fórmula para calcular la curvatura gaussiana es la siguiente:
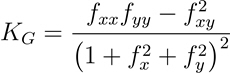
- Donde:
KG = Curvatura gaussiana
z = f(x,y)
Curvatura de Casorati
El parámetro de superficie Curvatura de Casorati mide la curvatura general de la superficie. Puede ser cero o cualquier otro número positivo. Los valores positivos altos indican áreas de curva pronunciada en varias direcciones.
La fórmula para calcular la curvatura de Casorati es la siguiente:
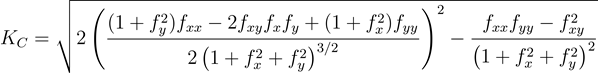
- Donde:
KC = Curvatura de Casorati
z = f(x,y)
Tipos de curvaturas básicas y combinatorias
La curvatura tangencial (curva de nivel normal), la curvatura de perfil (línea de pendiente normal) y la torsión geodésica de curvas de nivel se consideran tipos de curvaturas básicas porque se pueden expresar otras curvaturas como una combinación de ellos. En la terminología de Minár et al (2020), se describen como el trío básico.
Además de las expresiones proporcionadas arriba para Curvatura media, Curvatura gaussiana y Curvatura de Casorati, estas curvaturas también se pueden calcular como una combinación del trío básico.
La fórmula para calcular la curvatura media es la siguiente:
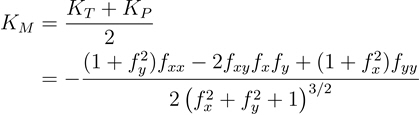
- Donde:
KM = Curvatura media
KT = Curvatura (curva de nivel normal) tangencial
KP = Curvatura (línea de pendiente normal) de perfil
z = f(x,y)
La fórmula para calcular la curvatura gaussiana es la siguiente:
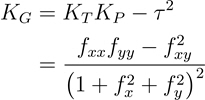
- Donde:
KG = Curvatura gaussiana
KT = Curvatura (curva de nivel normal) tangencial
KP = Curvatura (línea de pendiente normal) de perfil
T = Torsión geodésica de curvas de nivel
z = f(x,y)
La fórmula para calcular la curvatura de Casorati es la siguiente:
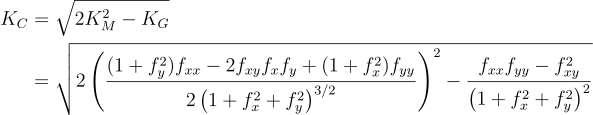
- Donde:
KC = Curvatura de Casorati
KM = Curvatura media
KG = Curvatura gaussiana
z = f(x,y)
Comparación con los algoritmos de las herramientas de curvatura anteriores
La herramienta Parámetros de superficie utiliza algoritmos de curvatura diferentes de los que emplea la herramienta Curvatura, además de geodesia matemática en los cálculos, por lo que no debe hacerse una comparación directa de los resultados de estas dos herramientas. Los tipos de curvatura de la herramienta Parámetros de superficie, curvatura (línea de pendiente normal) de perfil y curvatura (curva de nivel normal) tangencial, son curvaturas geométricas auténticas (Minár et al. 2020). La curvatura media de la herramienta Parámetros de superficie es el promedio de la curvatura mínima y máxima en ese punto. Los tipos Perfil y Plano de la herramienta de Curvatura son derivados direccionales; no miden en realidad la curvatura geométrica de la superficie en una ubicación (Zevenbergen y Thorne 1987). El signo (positivo o negativo) de la curvatura (línea de pendiente normal) de perfil de la herramienta Parámetros de superficie es contrario al de la curvatura de perfil de la herramienta Curvatura. La herramienta Parámetros de superficie basa el cálculo en el espacio geodésico y la herramienta Curvatura utiliza coordenadas planas y matemáticas. La herramienta Parámetros de superficie puede ajustarse a una superficie cuadrática o bicuadrática, mientras que la herramienta Curvatura solo admite superficies bicuadráticas.
Distancia de vecindad
El valor de Distancia de vecindad es la distancia cartográfica desde el centro de la celda de procesamiento actual hasta el centro de un vecino ortogonal. Una distancia de vecindad menor captura más variabilidad local en el paisaje, lo que resulta en características de entidades de paisaje más pequeñas. Con datos de elevación de mayor resolución, una distancia de vecindad mayor puede ser más apropiada debido a un error de escala fina (ruido) en los datos que no refleja los procesos de forma de suelo de interés, o porque la forma de suelo de interés es más reconocible a mayores distancias.
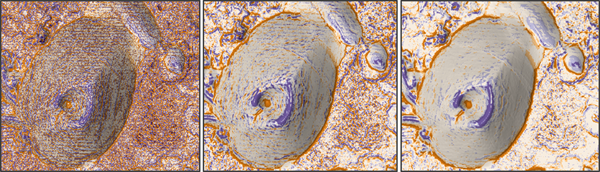
El siguiente ejemplo utilizó un modelo digital de superficie (DSM) de resolución de 5 metros que presentaba ruido perceptible y artefactos de división que se muestran en el resultado de curvatura de perfil (línea de pendiente normal). La primera imagen utilizó la ventana predeterminada de 3 x 3 o una distancia de vecindad de 5 metros, la segunda imagen es una ventana de celda de 9 x 9 o una distancia de vecindad de 20 metros, y la tercera imagen utilizó una ventana de celda de 15 x 15 o una distancia de vecindad de 35 metros. En este ejemplo, con la creciente distancia de vecindad, las entidades más importantes o principales del paisaje se vuelven más claras y los artefactos de ruido y división son menos visibles. Aunque una distancia de vecindad más grande siempre producirá menos ruido, la distancia más apropiada dependerá del tamaño de celda de los datos y el tamaño de las entidades de forma de suelo que sean importantes para la aplicación.
La distancia de vecindad más pequeña es igual al tamaño de celda del ráster de entrada. La distancia de vecindad más grande multiplica por siete el tamaño de celda, lo que resulta en una ventana de celda de 15 x 15. Cualquier distancia especificada que sea superior a siete veces el tamaño de celda resultará en una ventana de celda de 15 x 15.
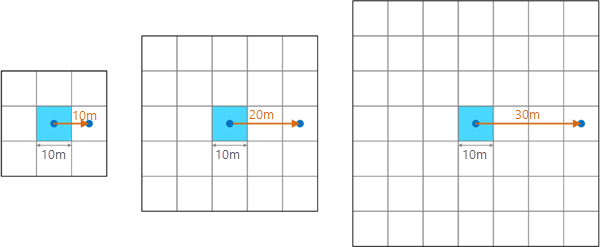
Si se especifica una distancia de vecindad que no resulta en un intervalo impar de tamaños de celda, se redondeará al siguiente intervalo de tamaños de celda. Por ejemplo, en la ilustración que aparece arriba, si se especificó una distancia de vecindad de 25 metros, se redondeará al siguiente intervalo de tamaños de celda, 30 metros (tres veces el tamaño de la celda), lo que resulta en una ventana de celda de 7 x 7.
Si los datos de elevación presentan una resolución espacial mucho más fina que la necesaria para analizar las formas de suelo de interés, una alternativa a la opción de la ventana de vecindad es remuestrear o agregar los datos a un tamaño de celda mayor que sea más apropiado para la aplicación.
Los cálculos de los parámetros de superficie son sensibles al tamaño de la celda y a la distancia de vecindad. Wilson (2018) y Minár y otros (2020) ofrecen resúmenes eficaces y actualizados de los numerosos estudios acerca de este tema.
Vecindad adaptable
Cuando se selecciona, el parámetro Utilizar vecindad adaptable cambia la distancia de vecindad (tamaño de ventana o área) usada para calcular el parámetro de superficie, a fin de capturar mejor la variación relevante del paisaje. La herramienta determina automáticamente el tamaño de ventana apropiado calculando la desviación local de la elevación media (DEV) (Wilson y Gallant, 2000), basándose en los valores de todas las celdas del vecindario. Intenta utilizar el mayor tamaño de ventana posible, a la vez que reduce al mínimo la variabilidad de la superficie (James et al., 2014). El tamaño de ventana más grande utilizado se especifica en el parámetro Distancia de vecindad.
Al calcular el parámetro de superficie con un vecindario fijo, se utilizan todos los valores de celda del vecindario. Al calcular el parámetro de superficie con un vecindario adaptable, solo se utilizan nueve celdas (las celdas ortogonales y diagonales exteriores y la celda de procesamiento central) del vecindario.
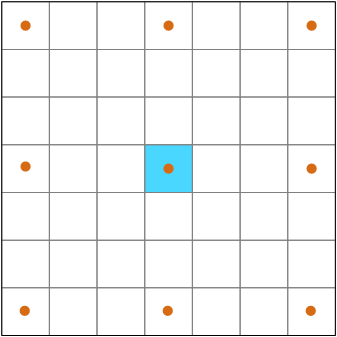
El vecindario adaptable resulta particularmente útil cuando se analiza un paisaje con entidades de terreno de tamaños muy variados, como grandes colinas con pequeños barrancos o cauces, de un DEM de alta resolución. En esta situación, puede utilizarse una distancia de vecindad pequeña, como 1 metro, para barrancos de calas y otra mayor de 10 o 15 metros para las colinas.
En la ilustración que aparece a continuación, una vecindad más pequeña es apropiado para el arroyo y el borde del acantilado; una vecindad más grande, para la transición de la colina a la llanura; y una vecindad aún mayor para la meseta homogénea casi llana.

Efecto de borde de la distancia de vecindad
Se asignará NoData a las celdas que rodean al borde exterior de la salida cuando no se disponga de información suficiente para el cálculo.
Cuando se usa la opción de vecindad adaptable, la extensión del ráster de salida se reducirá alrededor de su borde exterior en una celda.
Cuando se utiliza una distancia de vecindad fija mayor que el tamaño de celda de la entrada, la extensión del ráster de salida se reducirá de acuerdo con la distancia de vecindad utilizada. La cantidad de reducción puede calcularse de la siguiente forma: (ancho de ventana en píxeles - 1) / 2
Por ejemplo, si la distancia de vecindad resulta en el uso de una ventana de 7 x 7 celdas, el ráster de salida se reducirá alrededor de su borde exterior en tres celdas.
Cuadrática y bicuadrática
Existen dos tipos de superficies locales que se pueden ajustar a la ventana de vecindad: cuadrática y bicuadrática. La predeterminada es la cuadrática, que es la recomendada para la mayoría de datos y aplicaciones.
La superficie cuadrática es un ajuste por mínimos cuadrados de los puntos y no pasa exactamente por todos los puntos. Al no pasar exactamente a través de todos los puntos, usar la superficie cuadrática tiene el efecto de minimizar el impacto de los datos de la superficie con ruido, como una superficie LIDAR de alta resolución. Esto crea un resultado más representativo para todos los parámetros de superficie y es especialmente importante a la hora de calcular la curvatura.
La superficie cuadrática debería utilizarse al especificar un tamaño de vecindad mayor que el tamaño de celda, así como al utilizar la opción de vecindad adaptable.
La superficie bicuadrática ajusta los datos de las celdas de vecindad de forma exacta. Esta opción es adecuada para una superficie de entrada altamente precisa y carente de ruido aleatorio. Si la distancia de vecindad es mayor que el tamaño de celda ráster de entrada, se perderán las ventajas de precisión del tipo de superficie bicuadrática; en consecuencia, se debe dejar la distancia de vecindad predeterminada (igual al tamaño de celda).
Transformación de coordenadas geodésicas
La herramienta Parámetros de superficie realiza sus cálculos en un sistema de coordenadas 3D geocéntricas, también llamado sistema de coordenadas centrado en la Tierra, Tierra fija (ECEF), teniendo en cuenta la forma de la Tierra como un elipsoide. La forma en que esté proyectado el dataset no afecta al resultado del cálculo. Se utilizarán las unidades z del ráster de entrada si están definidas en la referencia espacial. Si la referencia espacial de la entrada no define las unidades z, deberá hacerlo con el parámetro de unidad z.
El sistema de coordenadas de ECEF es un sistema de coordenadas cartesianas dextrógiro 3D cuyo origen es el centro de la Tierra, donde cualquier ubicación se representa mediante coordenadas X, Y y Z. Consulte la figura siguiente para ver un ejemplo de una ubicación de destino T expresada con coordenadas geocéntricas.
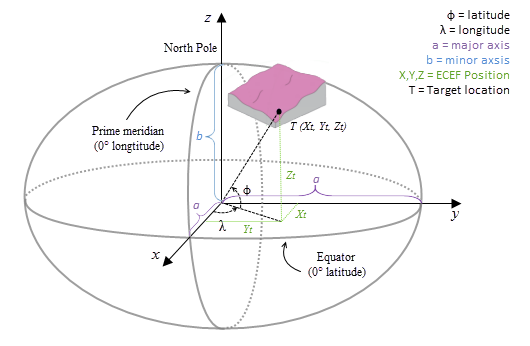
El ráster de la superficie se transforma desde el sistema de coordenadas de entrada en un sistema de coordenadas geocéntricas 3D.
El cálculo geodésico utiliza una coordenada X, Y, Z que se calcula según sus coordenadas geodésicas (latitud φ, longitud λ, altura h). Si el sistema de coordenadas del ráster de superficie de entrada es un sistema de coordenadas proyectadas (PCS), el ráster se reproyecta primero a un sistema de coordenadas geográficas (GCS) donde cada ubicación tiene una coordenada geodésica. A continuación, se transforma en el sistema de coordenadas de ECEF. La altura h (valor z) es la altura de elipsoide asociada a la superficie de elipsoide. Consulte el gráfico de la ilustración a continuación.
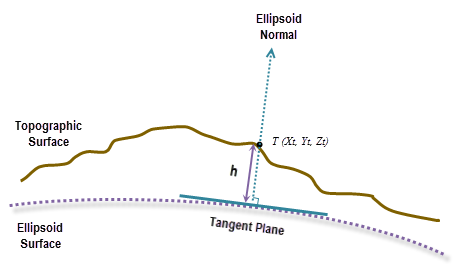
Para transformar a coordenadas de ECEF desde una coordenada geodésica (latitud φ, longitud λ, altura h), utilice las fórmulas siguientes:
X = (N(φ) + h) * cos(φ) * cos(λ)Y = (N(φ) + h) * cos(φ) * sin(λ)Z = (b2 / a2 * N(φ) + h) * sin(φ)- Donde:
N(φ) = a2 / √( a2 * cos(φ)2 + b2 * sin(φ)2)φ = latitud
λ = longitud
h = altura de elipsoide
a = eje mayor del elipsoide
b = eje menor del elipsoide
La altura h de elipsoide se expresa en metros en las fórmulas anteriores. Si la unidad z del ráster de entrada se especifica en otra unidad, se transformará internamente a metros.
Lectura recomendada
Para una comprensión más profunda de los métodos de análisis de la superficie y sus aplicaciones, consulte las referencias que aparecen a continuación. Además, tanto Hengl y Reuter (2008) como Wilson (2018) ofrecen una amplia catalogación de estas y otras muchas técnicas de análisis del terreno y sus aplicaciones. Minár y otros (2020) ofrecen una amplia sinopsis y una comparativa de obras anteriores relativas a la curvatura de la superficie terrestre, con aclaraciones y definición de numerosos tipos de curvatura.
Referencias
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Sección 10.2.1. p. 282.
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.
Crane K., 2018. Discrete Differential Geometry: An Applied Introduction. Notices of the AMS, Communication. https://www.cs.cmu.edu/~kmcrane/Projects/DDG/paper.pdf
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.
E.J.Krakiwsky, and D.E.Wells, 1971. Coordinate Systems In Geodesy (GEODESY AND GEOMATICS ENGINEERING, UNB), LECTURE NOTES, n.º 16, 1971, pp. 18-38
Hengl T. y Reuter H. 2008. Geomorphometry Concepts, Software, Applications. Elsevier.
James D.E., M.D. Tomer, S.A. Porter. 2014. Trans-scalar landform segmentation from high-resolution digital elevation models. Póster presentado en la Conferencia anual de usuarios de ESRI; julio de 2014; San Diego, CA.
Lancaster, P. and Šalkauskas, K. Curve and Surface Fitting: An Introduction. London: Academic Press, 1986.
Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY), Vol. 60, No 2, 2011, pp. 145-159
Minár, J., Evans, I. S., & Jenčo, M. (2020). A comprehensive system of definitions of land surface (topographic) curvatures, with implications for their application in geoscience modelling and prediction. Earth-Science Reviews, 103414. https://doi.org/10.1016/j.earscirev.2020.103414
Wilson J.P and Gallant, J.C. (Eds.) 2000. Terrain Analysis: Principles and Applications. John Wiley & Sons, Inc.
Wilson J.P 2018. Environmental Application of Digital Terrain Modeling. John-Blackwell, Inc.
Zevenbergen, L. W., and C. R. Thorne. 1987. Quantitative Analysis of Land Surface Topography. Earth Surface Processes and Landforms 12: 47–56.