Available with Image Server
Инструменты Накопление расстояния и Распределение по расстоянию заменяют устаревшие инструменты стоимостного расстояния. Эти новые инструменты измеряют стоимостное расстояние во всех направлениях, формируя непрерывную накопленную поверхность вместо поиска путей по сети из центров ячеек Вы можете создать выходную поверхность накопления стоимости на основе фрагментов поверхности и других параметров. Как и с другими поверхностями, вы можете получить более полный анализ результатов, добавив изолинии (линии одинакового накопления стоимости), визуализировав их в 3D, а затем добавив к визуализации распределение водосборных областей. Обычно такие поверхности строятся для идентификации путей с наименьшей стоимостью, которые, соответственно, являются путями в направлении самого крутого спуска.
Поверхность накопления стоимости
Алгоритм, используемый в этом инструменте, формирует поверхность на основании данных уклона.
Подход формирования поверхности
Инструменты Накопление расстояния и Распределение по расстоянию определяют наименьшую накопленную стоимость не основываясь на перемещении по сети. Выходной растр накопления стоимости представляет собой поверхность неизвестной формы. Вы изучаете эту форму, основываясь только на информации о значениях уклона для каждой ячейки в изучаемой области. Такой подход основан на концепции дифференциальной геометрии, чтобы вычислить истинное расстояние и стоимость по всем направлениям.
Поверхность накопления стоимости отвечает на три важных вопроса:
- Где стоимость растет быстрее, в зависимости от расстояния?
- Какие ячейки источника ближе всего к ячейке, не являющейся источником?
- Как пролегает путь между ячейкой не-источником к ближайшей ячейке-источнику?
Вы можете использовать 3D-представления и изолинии для выходной поверхности, чтобы найти ответы на эти вопросы. Вы можете использовать инструменты Распределение по расстоянию и Оптимальный путь как линия, чтобы получить более точные ответы.
В разделе ниже описаны отношения между простой входной стоимостной поверхностью сопротивления и выходной поверхностью накопления стоимости.
Входная стоимостная поверхность сопротивления
Допустим, у вас есть простая стоимостная поверхность сопротивления, где в центральной области стоимость перемещения - 3, в средней области стоимость перемещения - 2, и по краям - стоимость перемещения - 1.

3D-интерпретация поможет понять отношения между простой входной стоимостной поверхностью сопротивления и выходной поверхностью накопления стоимости. Высота поверхности в ячейке c - сумма уклонов входного растра стоимости, умноженная на расстояния, для которых эти уклоны рассчитаны (h = 3 * d1 + 2 * d2 + 1 * d3).
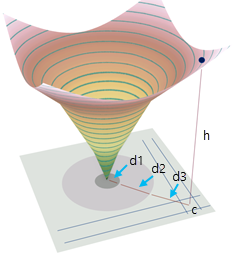
Плоскостное представление той же выходной поверхности показывает, как изолинии отображают изменения накопления стоимости. Значения уклона и экспозиции в местоположении ячейки тоже показаны. Экспозиция (направление самого крутого спуска всегда под прямым углом к изолинии.

Встроенная наименьшая накопленная стоимость
Более сложны пример описан ниже. Накопленная стоимость (высота) в ячейке, не являющейся источником, формируется от источника, движение от которого в эту ячейку будет осуществлено с наименьшей стоимостью.
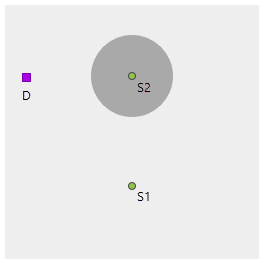
Стоимостной растр состоит из двух значений - 1 (светлый), и 3 (темно-серый). Точки источников S1 и S2. Ячейка D, которая не является источником, ближе к S1 в терминах накопления стоимости.
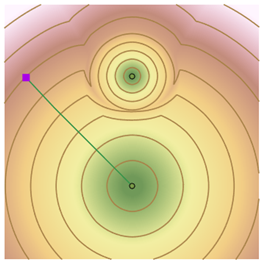
Добавление изолиний к поверхности накопления стоимости поможет визуализировать, насколько быстро меняется стоимость по мере перемещения дальше от источника. Начиная от местоположения (не источника) и перемещаясь под прямым углом к изолиниям, вы двигаетесь обратно в сторону ближайшего источника. Путь не ведет к ближайшему с точки зрения геометрии источнику, так как вокруг него область наивысшей стоимости перемещения.
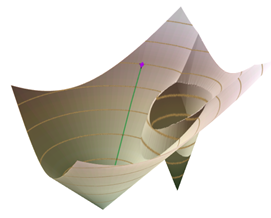
Ниже 3D-представление той же самой поверхности наименьшей накопленной стоимости перемещения. Поверхность вокруг источника с высокой стоимостью значительно круче (стоимость накапливается быстрее). Минимальная стоимость перемещения будет только для максимально близко расположенного источника. Для всех других ячеек в изучаемой области, поверхность наименьшей стоимости перемещения относится к источнику слева.
Определение регионов как водосборных областей
Хотя входная стоимостная поверхность сопротивления и выходная поверхность накопления стоимости стали более сложными, вы все равно можете использовать изолинии, уклон и экспозицию, чтобы лучше понять поведение поверхностей накопления стоимости. В дополнение, можно использовать функцию распределения регионов вокруг источников как водосборных областей для выходной поверхности накопления стоимости. Все пути с наименьшей стоимостью внутри этих регинов ведут к одному и тому же источнику. Распределение водосборных областей в комбинации с изолиниями и 3D-представлением на примере ниже.
Более сложные поверхности накопления стоимости, например, поверхность времени перемещения, можно визуализировать более точно в 2D и в 3D, используя изолинии (изохроны, в этом случае).
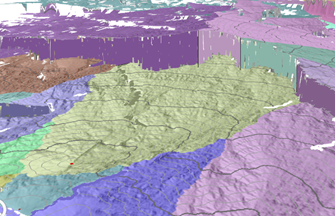
Ниже 3D-представление той же поверхности. Скалы на заднем плане - это барьеры, вызванные наличием реки.
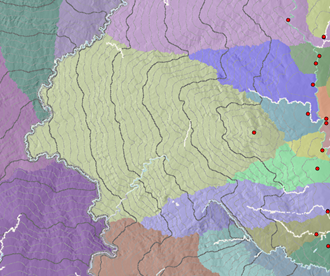
Пути с наименьшей стоимостью идут вниз по поверхности накопления стоимости к источнику, который задает зону распределения (водосборную область), как показано на следующем рисунке:
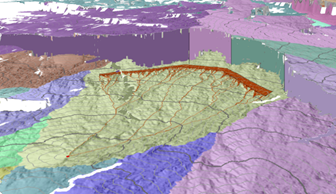
Алгоритм формирования поверхности расширяет алгоритм использования сети.
Для нахождения поверхности стоимости только на основе значений максимального уклона в каждой ячейке, вы можете также использовать алгоритм формирования поверхности. Этот алгоритм схож с алгоритмом кратчайшего пути, который используется в устаревших инструментах расчета стоимостного расстояния, но теперь в нем присутствует дополнительный шаг для аппроксимации накопления стоимости, что позволяет уйти от перемещения в одном из восьми направлений по сети, соединяющей центры ячеек. Это называется Эйкональный шаг. Краткое описание методики приведено ниже, более подробную информацию см. в статье Sethian, 1999.
Для понимания этого алгоритма в контексте, вы будете вычислять накопленную стоимость z5 для центральной ячейки. Допустим, вы знаете все значения накопления стоимости в окрестности zi. Также, из входного растра стоимости, вы знаете значение уклона S в центральной ячейке.
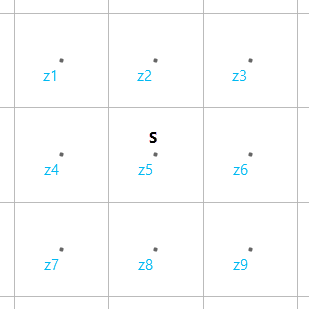
Например, одна аппроксимация для z5 может быть вдоль диагонали, соединяющей z3 и z5, где z5 = z3 + 1.4 * размер ячейки S, как показано на рисунке ниже. В этом примере S — значение из входного растра стоимости — интерпретируется как уклон для треугольника abc. Для всех таких аппроксимаций, основанных на сетевом алгоритме, для расчета накопления стоимости в z5 используется только значение уклона в z5. Это отличается от устаревшего сетевого алгоритма, в котором использовалась средняя стоимость для пары ячеек.
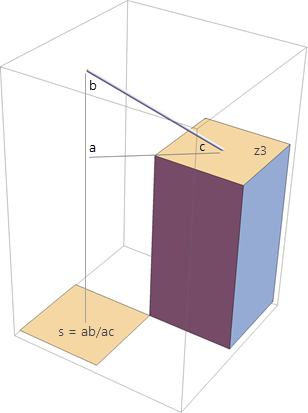
Может быть выполнено восемь сетевых аппроксимаций, включая четыре, которые используют пары существующих значений высот, как показано в последовательности из трех рисунков ниже. В этом случае значение входного стоимостного растра в ячейке z5 интерпретируется как амплитуда S градиента плоскости, проходящей через две известные точки и неизвестную высоту z5. Используя это отношение, вы можете получить решение для z5. Это Эйкональный шаг.
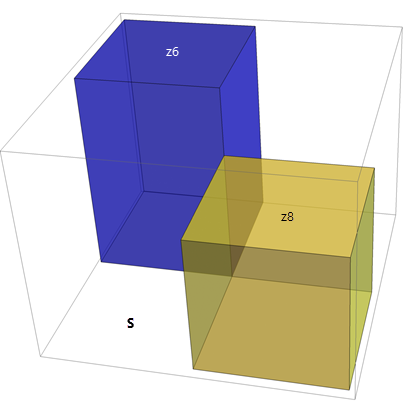
Амплитуда градиента плоскости вычислена.
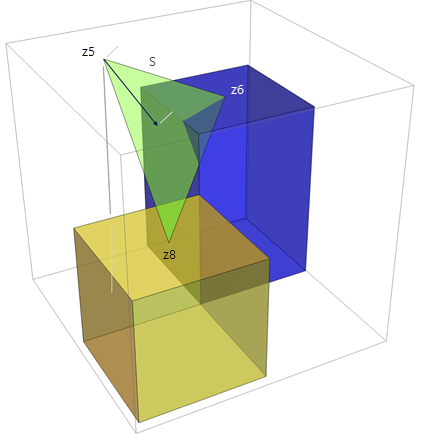
Вычисляется направление градиента.
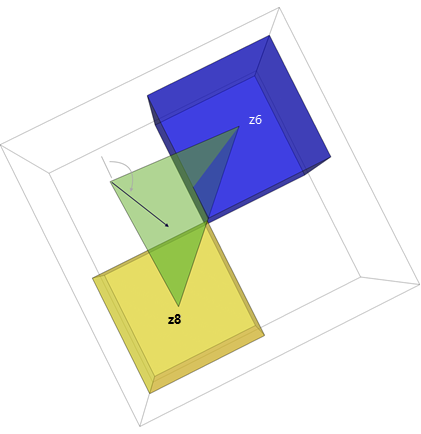
Эйкональный шаг также учитывает информацию экспозиции для z5, которая называется обратное направление.
Теперь у нас двенадцать аппроксимаций для высоты в центральной ячейке. Минимальная из них выбирается и записывается как значение накопления стоимости z5 для центральной ячейки. Если вы указали расчет растра обратного направления, экспозиция градиента (описанная в предыдущих разделах) записывается для соответствующего местоположения в выходном растре обратного направления.
Этот процесс повторяется для каждой ячейки, каждый раз после получения значения высоты из окрестности. В какой-то момент значения высот перестают меняться, и алгоритм прерывается. Начальные высоты предоставляются источниками - это либо ноль, или начальное значение накопления для каждого источника. Остальные начальные значения высот определены как бесконечность. Подробную информацию см. в публикации Sethian (1999). В применении Esri это комбинация методик, описанная в статьях Sethian (1999) и Zhao (2004).
Таким образом, начиная с уклона каждой ячейки, эти шаги формируют как высоту поверхности накопления стоимости, так и направление наиболее крутого спуска.
Пути наименьшей стоимости
Пути наименьшей стоимости следуют направлению самого крутого спуска по поверхности накопления стоимости. Это направление, для одной ячейки, показано выше, на рис. 8. Выходной растр обратного направления хранит направления для каждой ячейки. Вы можете использовать инструмент Оптимальный путь как линия, с растром обратного направления в качестве входного, чтобы нанести эти пути, начиная от любой ячейки, не являющейся источником.
На рисунке ниже показан изогнутый путь с наименьшей стоимостью, который начинается от ячейки - не источника d (голубого цвета) в правом верхнем углу, и следует к лежащей ниже ячейке-источнику s. Хотя d геометрически ближе к верхнему источнику, из-за высокой стоимости перемещения вокруг источника, дешевле следовать к источнику s по изогнутому пути.
Назначение d - квадрат голубого цвета. Путешественник перемещается по области наименьшей стоимости к источнику, достижение которого обходится дешевле, огибая источник, окруженной областью с высокой стоимостью перемещения.
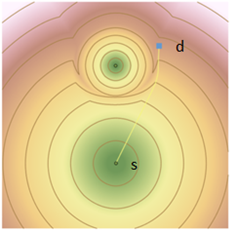
Хотя может показаться, что название не соответствует ожидаемому, входные местоположения для построения пути с наименьшей стоимостью называются назначениями. Источники используются для формирования поверхности, и представляют местоположения, в которых пути с наименьшей стоимостью завершаются.
Зоны распределения вокруг источников дополнительно уточняют, что путь с наименьшей стоимостью от назначения будет следовать к нижнему источнику, а не к верхнему. Далее, мы увеличим выбранную область, чтобы показать, как интерпретируются ячейки в растре обратного направления.
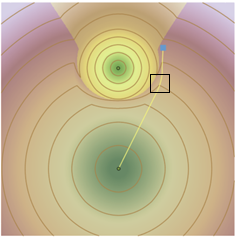
Решетка, соединяющая центры ячеек обратного направления показана темно серым цветом. Границы ячеек показаны светло-серым цветом, а значения ячеек отображены стрелками азимутального направления. Поскольку путь с наименьшей стоимостью пересекает линии решетки, он использует азимут в ближайшей ячейке обратного направления в направлении движения и, таким образом, обновляет направление перемещения по пути. Значение направления в ячейке a, расположенной рядом с самой верхней вершиной пути будет использовано для определения направления следования при выходе из этой вершины. Следующая линия решетки, которая будет пересечена при следовании, расположена рядом с ячейкой b, соответственно азимут в ней будет использован при выходе из второй вершины, и так далее.
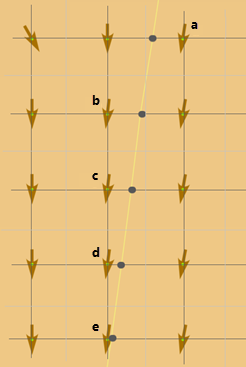
Обобщая все вышеизложенное, можем заключить, что пути с наименьшей стоимостью начинаются и заканчиваются в центрах ячеек. Остальные вершины пути могут быть в любом месте решетки вертикальных и горизонтальных линий, проходящих через центры ячеек.
Вычисление эффективного уклона
Значения уклона, описываемые выше, используются не сразу считываются из входного стоимостного растра сопротивления. Есть несколько других входных значение, которые, в совокупности, определяют эффективный уклон, используемый в алгоритме формирования поверхности. Подробное описание этих входных данных, включая важность учета направления перемещения через ячейку и направление движения как от, так и к источнику, описаны в следующих разделах. Здесь мы сосредотачиваемся на понимании того, как эти входные данные используются алгоритмом формирования поверхности. Входные данные для этого алгоритма:
- Входное стоимостное сопротивление, C
- Входная поверхность, S
- Коэффициент стоимости поверхности, M
- Функция горизонтального фактора, HF
- Функция вертикального фактора, VF
Эффективный уклон, используемый в алгоритме формирования поверхности, вычисляется по формуле:
Эффективный уклон = C * S * M * HF * VF
Это значение затем умножается либо на размер ячейки, либо на квадрат размера ячейки (2) * и добавляется к существующему значению высоту для получения одного из восьми аппроксимаций сетевого направления. Более сложная функция вычисления эффективного уклона используется для получения аппроксимации высоты для Эйконального шага.
Эффективный уклон должен измерятся в единицах накопления стоимости, деленных на линейные единицы (отношение) Например, если ваша поверхность накопления стоимости содержит измерения времени перемещения в часах, а размер ячейки определен в метрах, эффективный уклон должен быть выражен в единицах час/метр.
Так как эффективный уклон является комбинацией нескольких условий, вы должны быть уверены, что единицы измерения отдельных условия скомбинированы корректно в правильные единицы эффективного уклона. Например, если вы используете только простой стоимостной растр сопротивления для описания времени перемещения независимо от направления, единицы измерения значений ячеек стоимостного растра сопротивления должны быть час/метр. Или, если вы также используете функцию пешего прохода Тоблера как функцию вертикального фактора, эта функция пешего прохода будет выражена в единицах измерения час/метр, а ваша стоимостная поверхность сопротивления, если она присутствует, должна интерпретироваться как вес без единиц измерения. Вы должны тогда убедиться, что значения ячеек стоимости сопротивления должны интерпретироваться именно таким образом. Другими словами, ваша вертикальная функция и стоимостная функция не могут вместе участвовать в формировании цены.
Вы не управляете напрямую входной поверхностью (S). Это безразмерное значение веса, которое растягивается на размер ячейки, чтобы покрыть фактическое 3D-расстояние по поверхности между центрами ячеек. На рис. 2 алгоритм формирования поверхности вычисляет высоту z5 для центральной ячейки, выполняя множественную аппроксимацию этой высоты, используя значение уклона из входного стоимостного растра сопротивления в центральной ячейке, вместе с известными высотами для соседних ячеек.
Барьеры, связанные ребрами
Барьеры в инструментах Накопление расстояния и Распределения по расстоянию - это входные ячейки, через которые перемещение невозможно. Они представлены как ячейки NoData во время вычислений. Они указываются либо открыто, как параметр инструмента или закрыто, как значения NoData в одном из других входных растров (например в стоимостном растре сопротивления). В первом случае они растеризуются и меняются на NoData в стоимостном растре. Поскольку алгоритм формирования поверхности не может понизить оценку высоты барьерной ячейки, он находит способ обойти ее.
Алгоритм формирования поверхности использует все 8 соседних ячеек для нахождения оценки высоты. Ячейки-барьеры, связанные углами, не мешают использованию соседней по диагонали ячейки для получения оценки высоты. На рисунке ниже оценка высоты для z5 может быть получена из z3, хотя ячейки z2 и z6 являются барьерами.
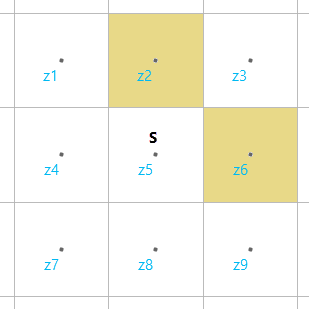
Если ячейки z2 и z6 составляют часть линейного барьерного объекта, такого как канал или река, такое поведение будет игнорировать барьер. Чтобы предотвратить это, алгоритм формирования поверхности отдает предпочтение связанным барьерным ячейкам по сравнению со связанными ячейками, не являющимися барьерами. Это означает, что во входной стоимостной растр добавляются ячейки NoData, для гарантии того, что все имеющиеся барьерные ячейки содержат общие ребра. На рисунке выше, и ячейка z5, и ячейка z3 могут стать барьерными ячейками.
При использовании барьеров в своем анализа согласуйте поведение и скорректируйте размер ячейки анализа таким образом, чтобы связность вокруг барьеров сохранялась. Вы можете использовать инструмент Фокальная статистика для расширения растровой версии линейных объектов, чтобы использовать их либо как барьеры, либо как линейную сеть, которая не должна интерпретироваться как смежные барьерные ячейки.
Список литературы
Douglas, D. "Least-cost Path in GIS Using an Accumulated Cost Surface and Slopelines", Cartographica: The International Journal for Geographic Information and Geovisualization, 1994, Vol. 31, No. 3, DOI: 10.3138/D327-0323-2JUT-016M
Goodchild, M.F. "An evaluation of lattice solutions to the problem of corridor location", Environment and Planning A: Economy and Space, 1977, vol. 9, pages 727-738
Sethian, J.A. Level Set Methods and Fast Marching Methods (Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science) 2nd Edition, Cambridge University Press, 2nd edition (June 1, 1999)
Warntz, W. "Transportation, Social Physics, and the Law Of Refraction", The Professional Geographer, 1957, Vol. 9, No. 4, pp. 2-7.
Zhao, H. "A fast sweeping method for Eikonal equations", Mathematics of Computation, 2004, Vol. 74, No. 250, pages 603-627