Ajustar a distância encontrada usando um fator vertical

Disponível com Image Server

Uma vez calculada a distância em linha reta ajustada, você pode usar o fator vertical para controlar a taxa na qual a distância é encontrada. Você pode usar a superfície de custo, características do movedor, e o fator horizontal para controlar a taxa também.

O fator vertical responde pelo esforço de deslocamento pelas encostas da paisagem. Esse esforço afeta como a distância é encontrada. Subir uma ladeira pode exigir mais esforço, descer uma ladeira requer menos esforço e cruzar encostas fica em algum lugar no meio. A modificação da distância em linha reta ajustada para esse esforço ajuda a capturar a taxa na qual a distância é encontrada pelo viajante.

Menos energia é gasta ao descer uma ladeira para que o andarilho possa cobrir a distância mais rapidamente

Não confunda o fator vertical, que representa o esforço para superar inclinações, com a distância de superfície, que é um ajuste da distância em linha reta para a distância real que o viajante percorre ao se deslocar nas subidas e descidas da paisagem.

A inclinação geralmente é relevante para a análise da distância de custo. Intuitivamente, é mais caro superar encostas íngremes do que encostas mais planas. Normalmente, a ferramenta Parâmetros da Superfície é usada para gerar um raster de declividade; no entanto, às vezes esse raster de declividade é inserido incorretamente na superfície de custo.

A opção Declividade na ferramenta Parâmetros da Superfície calcula a taxa de alteração da elevação para cada célula do modelo digital de elevação (DEM). É o primeiro derivado de um DEM. Mas, como discutido acima, importa como a inclinação é encontrada ao se mover através de uma célula. O viajante pode evitar uma célula com uma inclinação acentuada em uma superfície de custo. Isso pode ser eficaz se o viajante estiver subindo aquela inclinação ao passar pela célula. No entanto, se o viajante estiver descendo ou atravessando essa inclinação ao se mover pela célula, a célula poderá ser preferida para a viagem.

Você pode contabilizar o esforço para superar a inclinação usando o raster de elevação no fator vertical. Não inclua o raster de inclinação na superfície de custo quando a direção em que a inclinação é encontrada for importante.

A direção na qual as inclinações são calculadas no fator vertical também pode ser alterada pelo parâmetro de característica da origem da direção de viagem. Ou seja, aproximar-se ou afastar-se de uma origem mudará a direção na qual o viajante entrará em uma célula e, como resultado, como a inclinação será encontrada.

A incorporação do fator vertical (VF) é um modificador multiplicador para os cálculos de distância em linha reta ajustados. Detalhes sobre como o fator vertical é calculado são fornecidos no tópico Algoritmo de acumulação de distância.

Exemplos de uso do fator vertical

O fator vertical pode ser usado em vários cenários, como os seguintes:

• Localizar uma nova trilha de caminhada entre dois acampamentos que seja mais longa, porém mais fácil de percorrer do que caminhar diretamente pelo caminho mais curto entre eles.
• Examinar os efeitos do sal espalhado nas estradas no inverno sobre a saúde da vegetação circundante. A vegetação descendente da estrada será mais impactada pelo escoamento.
• Determinar o movimento de uma criatura marinha que depende da mudança na concentração de salinidade.

Incorporar um fator vertical

Distance analysis can be divided conceptually into the following related functional areas:

• Calculate straight-line distance and optionally adjust the calculations with a barrier or surface raster.
• Após a distância em linha reta ser calculada, opcionalmente, determine a taxa em que a distância será encontrada por meio de uma superfície de custo, características da fonte, um fator vertical, e um fator horizontal. Crie o raster de distância acumulativa.
• Connect regions over the resulting accumulative distance surface using an optimal network, specific paths, or a corridor.

A partir da segunda área funcional, determine a taxa na qual a distância será encontrada através de um fator vertical conforme ilustrado abaixo. O cenário envolve um conjunto de quatro estações de guarda florestal (pontos roxos) e alguns rios (linhas azuis).

A distância de menor custo de cada célula até as estações de guarda florestal mais próximas incorpora uma barreira, raster de superfície e superfície de custo.

Para incorporar o esforço dos guardas florestais na superação dos desníveis, é especificado um fator vertical. A superfície de elevação é usada como raster vertical.

A distância de menor custo de cada célula até a estação de guarda florestal mais próxima, incorporando o fator vertical ao mapa acima com uma barreira, raster de superfície e superfície de custo. O fator vertical influencia o centro da área de estudo em particular.

Criar um raster de distância usando um fator vertical

Para criar um mapa de distância que incorpore um fator vertical, complete as seguintes etapas:

1. Abra a ferramenta Acumulação de Distância.
2. Forneça uma fonte para o parâmetro Raster de entrada ou o de dados de origem .
3. Nomeie o raster de acumulação de distância de saída.
4. Expanda a categoria Custos relativos ao movimento vertical.
5. Forneça um raster de fator vertical para o parâmetro Raster vertical de entrada.

   Esta entrada é usada para calcular a inclinação encontrada ao mover entre as células. Normalmente, um raster de elevação deve ser especificado.

   O parâmetro Fator vertical aparece.

6. Especifique as configurações para o parâmetro Fator vertical.

   Este parâmetro identifica o multiplicador a ser aplicado ao custo para ajustar o esforço de deslocamento pelas inclinações encontradas.

7. Clique em Executar.

O fator vertical afeta a taxa de distância encontrada

Para modificar a velocidade com que a distância é encontrada e contabilizar o esforço do viajante para superar as inclinações, internamente a ferramenta realiza duas ações:

• Calcula como a inclinação é encontrada ao mover de uma célula para a próxima. Isso é denominado ângulo de movimento relativo vertical (VRMA).
• Identifica como o VRMA modificará a taxa na qual a distância é encontrada.

Calcular o VRMA

O VRMA é o ângulo de inclinação da célula de processamento (a célula De) para a célula na qual o viajante está se movendo (a célula Para). A distância está sendo calculada na célula Para. As alturas a partir das quais as inclinações são calculadas são definidas pelo raster do fator vertical de entrada.

A inclinação é calculada usando a fórmula do teorema de Pitágoras de subida/descida. A base do triângulo necessária para determinar a inclinação é derivada da distância em linha reta ajustada. A altura é estabelecida subtraindo o valor da célula De do valor da célula Para. O ângulo resultante é o VRMA.

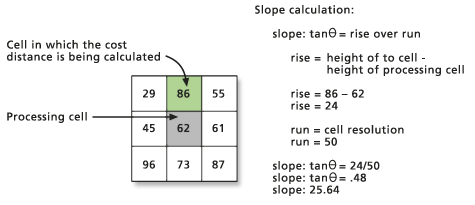
O VRMA é especificado em graus. A faixa de valores para o VRMA é de -90 a +90 graus, representando inclinações positivas e negativas.

Identificar o multiplicador VF

O valor de VRMA é então plotado no gráfico de fator vertical especificado para obter o multiplicador de fator vertical que será usado nos cálculos que determinam o custo para atingir a célula Para. O valor da distância a percorrer na célula é multiplicado pelo fator vertical identificado. Quanto maior o fator vertical, mais difícil o movimento. Um VF maior que 1 aumenta a distância de custo encontrada. Um VF menor que 1, mas maior que 0, permite que o motor encontre as distâncias em uma taxa mais rápida.

Por exemplo, o gráfico a seguir mostra a relação entre VF e VRMA para uma função VF linear:

A relação entre VF e VRMA é mostrada em um gráfico do tipo linear.

As funções do fator vertical que permitem capturar a interação do viajante com as inclinações que ele encontra são Binário, Linear, Linear Inverso, Linear Simétrico, Linear inverso simétrico, Cos, Sec, Cos-Sec, and Sec-Cos. Consulte a seção Informações adicionais abaixo para obter detalhes de cada função.

Anotação:

O fator vertical é um multiplicador. Tome cuidado ao especificar as unidades ao combinar o fator vertical com uma superfície de custo, características da origem ou um fator horizontal. Geralmente, quando uma superfície de custo é inserida, o fator vertical deve ser um ajuste multiplicador da taxa de unidades da superfície de custo. Se o tempo é a unidade para a taxa da superfície de custo, o fator vertical deve ser um modificador de tempo. Apenas um desses fatores pode definir as unidades para a taxa. Os outros fatores não têm unidade e seus valores são modificadores multiplicadores das unidades especificadas.

Aplicações de exemplo que usam um fator vertical

Aplicações de exemplo que usam um fator vertical estão descritas abaixo.

Criar um buffer de descida para entender o efeito do sal de inverno na vegetação

Você deseja identificar áreas que são inclinadas e a 50 metros de uma estrada pois essas áreas podem ser afetadas pelo escoamento de água salgada no inverno. Você deseja medir a distância ao longo da superfície do terreno. Você pode usar a configuração do fator vertical Binário para impedir que a ferramenta Acumulação de Distância identifique células que são mais altas que as células da estrada. Exemplos dos buffers de inclinação resultantes são mostrados abaixo.

As áreas que podem ser impactadas pelo escoamento de sal no inverno abaixo das estradas são identificadas. Usando a Acumulação de Distância com a configuração Binário do fator vertical, as células de inclinação dentro de uma distância de superfície de 50 metros das estradas são determinadas (sombreamento laranja).

Para comparação, uma seção diferente da estrada é usada para mostrar a diferença nos buffers em linha reta e apenas em inclinações, conforme mostrado abaixo.

Um buffer de distância em linha reta de 50 metros (sombreamento azul) sobreposto em um buffer de distância de superfície somente descida (sombreamento laranja). Este último é mais estreito em locais onde você não pode descer 50 metros.

Para criar um buffer de descida, complete as seguintes etapas:

1. Abra a ferramenta Acumulação de Distância.
2. Insira as estradas no parâmetro Dados de origem da feição ou raster de entrada.
3. Nomeie o valor Raster de acumulação de distância de saída.
4. Expanda a categoria Custos relativos ao movimento vertical.
5. Forneça um raster de elevação no parâmetro Raster vertical de entrada.
6. Defina Binário para o parâmetro Fator vertical.
7. Expanda a categoria Características da origem.
8. Defina o parâmetro Distância máxima de acumulação para 50 metros:
9. Clique em Executar.

Função de caminhada de Tobler

Você deseja calcular o tempo de caminhada na paisagem, enquanto ajusta a velocidade de caminhada com base na inclinação encontrada na direção da viagem. A função de caminhada de Tobler (1993) é um modelo empírico usado para realizar esse ajuste. No modelo, assume-se que a velocidade base de caminhada é de 6 km/h, o que é alcançado ao se deslocar ligeiramente para baixo (cerca de -3 graus).

Onde S é definido em termos da inclinação d (dado em graus), de modo que S = tan(d π/180)

A função de velocidade W se parece com o seguinte:

A função da velocidade de Tobler conforme uma função de inclinação em graus é expressa em km/h. A velocidade máxima de viagem de 6 km/h ocorre ao caminhar levemente em descidas.

Você deseja saber quanto tempo leva para percorrer uma determinada distância (uma célula), não o quão longe você pode viajar em um determinado período de tempo, então você precisa trabalhar com o recíproco da velocidade, denominado ritmo. O ritmo em horas por metro (pois as unidades da análise de distância horizontal são metros) é expresso, em vez de horas por quilômetro:

A função Ritmo se parece com o seguinte:

O recíproco de função da velocidade de Tobler é a função de ritmo, aqui expressa em horas por metro, plotada em função da inclinação em graus.

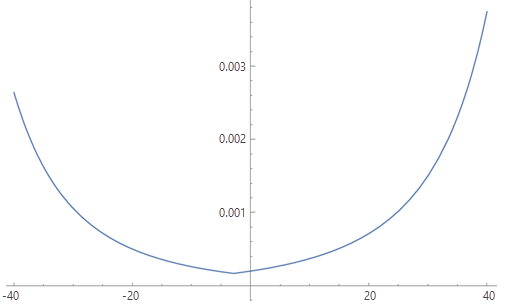
Determine o P(S) para um intervalo de valores de d e salve-os em uma tabela (mostrada na seção Tabela abaixo). A tabela pode então ser usada com a função de fator vertical da Tabela para fornecer um custo por célula que leva em conta a direção da viagem através de uma célula. O custo (no tempo) para percorrer uma célula em uma direção específica e encontrar uma inclinação d é P(S(d)) * tamanho da célula (em metros).

Para usar uma superfície de fricção de custo de entrada não direcional além da função de caminhada (ritmo) de Tobler na mesma análise, preste atenção às unidades de entrada de fricção de custo. Em cada célula, a ferramenta Acumulação de Distância multiplicará P(S) * (custo de entrada na célula), portanto, os valores não podem ter unidades de ritmo. Você pode modificar a função de ritmo de Tobler para ser apenas um peso (substitua o 6 por 1 se achar que isso é justificado empiricamente) ou usar pesos sem unidade em sua entrada de custo.

Informações adicionais

As seções a seguir fornecem informações adicionais sobre fatores verticais.

Fatores verticais

Para definir a função de fator vertical, você pode escolher um de uma lista de gráficos fornecidos ou pode criar uma função personalizada usando um arquivo ASCII. As seguintes funções de fator vertical estão disponíveis na ferramenta Acumulação de Distância:

Opções de fator vertical, modificadores e valores padrão

Função	Fator Zero	Ângulo de corte baixo	Ângulo de corte alto	Declividade	Potência	Potência cos	Potência sec
Binário	1	-30	30	N/A	N/A	N/A	N/A
Linear	1	-90	90	1.111E-02	N/A	N/A	N/A
Linear inverso	1	-45	45	-2.222E-02	N/A	N/A	N/A
Linear simétrico	1	-90	90	1.111E-02	N/A	N/A	N/A
Linear simétrico inverso	1	-45	45	-2.222E-02	N/A	N/A	N/A
Cos	N/A	-90	90	N/A	1	N/A	N/A
Seg	N/A	-90	90	N/A	1	N/A	N/A
Cos – Sec	N/A	-90	90	N/A	N/A	1	1
Sec – Cos	N/A	-90	90	N/A	N/A	1	1

Binário

Quando o VRMA é maior que o ângulo de corte baixo e menor que o ângulo de corte alto, o VF para mover entre as duas células é definido para o valor associado ao fator zero. Se o VRMA for maior que o ângulo de corte, o VF será definido como infinito. O ângulo de corte padrão é de 30 graus se nenhum for especificado.

Linear

Os VFs são determinados por uma linha reta no sistema de coordenadas VRMA-VF. A linha intercepta o eixo y, equivalente ao fator VF, no valor de fator zero. A inclinação da linha pode ser especificada usando o modificador Declividade. Se nenhuma declividade for identificada, o padrão será 1/90 (especificado como 0.01111). O ângulo de corte baixo padrão é de -90 graus e o ângulo de corte alto padrão é de 90 graus.

Linear inverso

Os VFs são determinados pelos valores inversos de uma linha reta no sistema de coordenadas VRMA-VF. A linha intercepta o eixo y, equivalente ao fator VF, no valor de fator zero. A inclinação da linha pode ser identificada se especificada com o modificador Declividade. Se nenhuma inclinação for identificada, o padrão será -1/45 (especificado como 0.02222). O ângulo de corte baixo padrão é de -45 graus e o ângulo de corte alto padrão é de 45.

Linear simétrico

Este fator vertical é composto por duas funções lineares relativas aos VRMAs que são simétricas ao eixo VF (y). Ambas as linhas interceptam o eixo y no valor VF associado ao fator zero. A inclinação das linhas é definida como uma única inclinação relativa ao VRMA positivo usando o modificador de fator vertical Declividade, que espelha os VRMAs negativos. A inclinação padrão é 1/90 (especificada como 0.01111). O ângulo de corte baixo padrão é -90, e o ângulo de corte alto padrão é 90.

Linear simétrico inverso

Esse fator vertical é o inverso da palavra-chave do fator vertical Linear simétrico. É composto por duas funções lineares inversas relativas aos VRMAs que são simétricas ao eixo VF (y). Ambas as linhas interceptam o eixo y no valor VF de 1. A inclinação das linhas é definida como uma única inclinação relativa ao VRMA positivo usando o modificador de fator vertical Declividade, que espelha os VRMAs negativos. A inclinação padrão é -1/45 (especificada como 0.02222). O ângulo de corte baixo padrão é -45, e o ângulo de corte alto padrão é 45.

Cos

O VF é determinado pela função co-seno do VRMA. O ângulo de corte baixo padrão é de -90 graus e o ângulo de corte alto padrão é de 90 graus. O valor Potência cos padrão é 1.0.

Sec

O VF é determinado pela função secante do VRMA. O ângulo de corte baixo padrão é de -90 graus e o ângulo de corte alto padrão é de 90 graus. O valor Potência sec padrão é 1.0.

Cos - Sec

Quando o VRMA é um valor de grau negativo, o VF é determinado pela função co-seno do VRMA. Se o VRMA for um valor de grau positivo, o VF será determinado pela função secante do VRMA. O ângulo de corte baixo padrão é de -90 graus e o ângulo de corte alto padrão é de 90 graus. Os valores Potência cos e Potência sec padrão é 1.0.

Sec - Cos

Quando o VRMA é um valor de grau negativo, o VF é determinado pela função secante do VRMA. Se o VRMA for um valor de grau positivo, o VF será determinado pela função co-seno do VRMA. O ângulo de corte baixo padrão é de -90 graus e o ângulo de corte alto padrão é de 90 graus. Os valores Potência sec e Potência cos padrão é 1.0.

Tabela

A tabela é um arquivo ASCII com duas colunas em cada linha.

A primeira coluna identifica o VRMA em graus e a segunda coluna identifica o VF. Cada linha especifica um ponto. Dois pontos consecutivos produzem um segmento de linha no sistema de coordenadas VRMA-VF. Os ângulos devem ser inseridos em ordem crescente e variam de -90 a 90. O fator VF para qualquer ângulo VRMA menor que o primeiro (menor) valor de entrada ou maior que a entrada final (maior) será definido como infinito. Um VF infinito é representado por -1 na tabela ASCII.

O seguinte é um exemplo de tabela ASCII de fator vertical: As unidades da primeira coluna são graus e as unidades da segunda coluna são horas por metro.

    -90  -1
    -80  -1
    -70   2.099409721
    -60   0.060064462
    -50   0.009064613
    -40   0.00263818
    -30   0.001055449
    -20   0.000500142
    -10   0.00025934
      0   0.000198541
     10   0.000368021
     20   0.000709735
     30   0.001497754
     40   0.003743755
     50   0.012863298
     60   0.085235529
     70   2.979204206
     80  -1
     90  -1

Modificadores de fator vertical

Você pode controlar ainda mais a função VRMA usando modificadores que permitem o refinamento de fatores verticais. Pode haver um ângulo limite tal que, se o VRMA o exceder, o custo será tão grande que se tornará uma barreira para viajar. Este limite é determinado como o ângulo de corte. O VF é atribuído ao infinito quando o VRMA excede esse valor.

O gráfico de fator vertical terá ângulos de corte inferior e superior em contraste com o gráfico de fator horizontal, que terá apenas um único ângulo de corte.

Usando esses modificadores, os ângulos de corte podem ser especificados para cada uma das funções, as curvas trigonométricas podem ser aumentadas por uma potência, o fator zero pode alterar a interceptação do eixo y para as funções não trigonométricas e a inclinação da linha nas funções lineares pode ser definida.

Fator Zero

Este modificador estabelece o fator vertical usado quando o VRMA é zero. Este fator posiciona a opção interceptar y da função especificada.

Ângulo de corte baixo

Esse modificador é o grau VRMA que define o limite inferior, abaixo do qual (menor que) os VFs são definidos como infinitos, independentemente das palavras-chave de fator vertical especificadas.

Ângulo de corte alto

Esse modificador é o grau VRMA que define o limite superior, além do qual (maior que) os VFs são definidos como infinitos, independentemente das palavras-chave de fator vertical especificadas.

Declividade

Este modificador identifica a inclinação das linhas retas no sistema de coordenadas VRMA-VF para as palavras-chaves Linear, Linear Inverso, Linear simétrico e Linear inverso simétrico. A declividade é especificada como a elevação ao longo do trecho (por exemplo, uma declividade de 30 graus é 1/30, especificada como 0,03333). Veja o diagrama Linear VRMA para um exemplo de uma função linear com uma inclinação de 1/90.

Potência

Este modificador é a potência à qual os valores serão elevados.

Potência cos

Este modificador é a potência à qual os valores não negativos na função Sec-Cos do VRMA e os valores negativos na função Cos-Sec do VRMA serão aumentados. O VF é determinado pelo seguinte:

VF = cos(VRMA)power

Potência sec

Este modificador é a potência à qual os valores não negativos na função Cos-Sec do VRMA e os valores negativos na função Sec-Cos do VRMA serão aumentados. O VF é determinado pelo seguinte:

VF = sec(VRMA)power

Nome da Tabela

Este modificador identifica o nome do arquivo ASCII que será usado com a palavra-chave Tabela do fator vertical.

Referências

Tobler, Waldo (1993) Três apresentações sobre análise e modelagem geográfica: Modelagem geográfica não isotrópica; Especulações sobre a Geometria da Geografia; e Análise Espacial Global (93-1) Recuperado de https://escholarship.org/uc/item/05r820mz