Available with Image Server
Eine der Hauptvoraussetzungen für das Ableiten hydrologischer Eigenschaften einer Oberfläche besteht darin, die Fließrichtung aus den einzelnen Zellen im Raster bestimmen zu können. Dies wird mit dem Werkzeug erreicht.
Dieses Werkzeug benötigt eine Fläche als Eingabe und erzeugt ein Raster mit der Fließrichtung aus den einzelnen Zellen als Ausgabe. Wenn die Option Ausgabe-Absenkungs-Raster gewählt wird, wird ein Ausgabe-Raster erzeugt, das das Verhältnis zwischen der maximalen Änderung in der Höhe von jeder Zelle in der Fließrichtung und der Pfadlänge zwischen den Zellenmittelpunkten zeigt, ausgedrückt als Prozentsatz. Wenn die Option Abfluss von Randzellen nach außen erzwingen aktiviert ist, fließen alle Zellen am Rand des Oberflächen-Rasters vom Oberflächen-Raster nach außen.
Es gibt acht gültige Ausgabe-Richtungen, die sich aus den acht benachbarten Zellen, in die der Abfluss erfolgen kann, ergeben. Dies wird üblicherweise als D8-Fließmodell bezeichnet und geht auf einen Ansatz zurück, der in Jenson und Domingue (1988) vorgestellt wird.
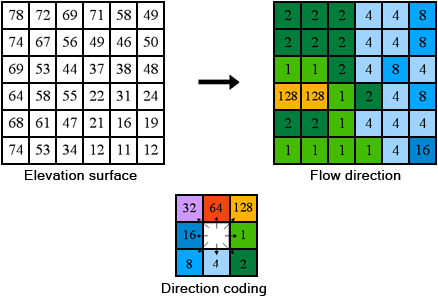
Berechnen der Fließrichtung unter Verwendung der D8-Methode
Bei der D8-Methode wird die Fließrichtung durch die Richtung des steilsten Abgangs oder maximalen Abfalls von jeder Zelle bestimmt (Jenson und Domingue, 1988). Dieser Wert wird wie folgt berechnet:
maximum_drop = change_in_z-value/distanceDie Entfernung zwischen Zellenmittelpunkten wird berechnet. Beispielsweise beträgt bei der Zellengröße 1 die Entfernung zwischen zwei orthogonalen Zellen 1, und die Entfernung zwischen zwei diagonalen Zellen entspricht der Quadratwurzel von 2. Wenn der maximale Abfall in mehrere Zellen gleich ist, wird die Nachbarschaft vergrößert, bis der steilste Abfall gefunden wird.
Sobald die Richtung des steilsten Abfalls gefunden ist, wird die Ausgabe-Zelle mit dem Wert, der diese Richtung darstellt, codiert.
Wenn alle Nachbarn höher sind als die bearbeitete Zelle, wird sie als Rauschen betrachtet. Sie wird bis auf den niedrigsten Wert der Nachbarn aufgefüllt und verfügt über eine Fließrichtung zu dieser Zelle. Wenn eine aus einer Senke bestehende Zelle sich jedoch neben der physischen Kante des Rasters befindet oder mindestens eine NoData-Zelle als Nachbarn hat, wird sie aufgrund unzureichender Nachbarschaftsinformationen nicht gefüllt. Um als eine richtige Senke aus einer Zelle betrachtet zu werden, müssen alle Nachbarschaftsinformationen vorhanden sein.
Wenn zwei Zellen ineinander fließen, handelt es sich um Senken mit einer undefinierten Fließrichtung. Diese Methode der Ableitung der Abflussrichtung aus einem digitalen Höhenmodell (DEM) wird in Jenson und Domingue (1988) dargestellt.
Zellen, die Senken darstellen, können mit dem Werkzeug Senke identifiziert werden. Um eine genaue Darstellung der Fließrichtung über eine Oberfläche zu erhalten, sollten die Senken gefüllt werden, bevor das Werkzeug Fließrichtung verwendet wird.
Berechnen der Fließrichtung unter Verwendung der MFD-Methode
Bei der MFD-Methode wird die Fließrichtung über alle niedrigeren Nachbarn hinweg partitioniert (Qin et al., 2007). Die Fließmenge, die die einzelnen niedrigeren Nachbarn erhalten, wird als Funktion des maximalen Neigungsgradienten geschätzt, die lokale Terrainbedingungen berücksichtigt. Der Ausdruck für die Schätzung der MFD lautet wie folgt:
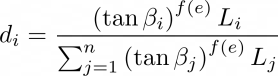
Wobei gilt:
- di = Teil des Abflusses aus jeder Zelle, der in die Zelle i fließt
- f (e) = Exponent, der sich an die lokalen Terrainbedingungen anpasst und angegeben wird durch
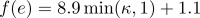
- β = Neigungswinkel (in Radiant)
- n = Anzahl der Zellen, die in die Zelle i fließen
- Li, Lj = Angepasster Faktor zur Berücksichtigung der Entfernung zwischen der Verarbeitungszelle und den orthogonalen und diagonalen Zellen
- κ = Maximaler Abfall über Zellen hinweg, die in Zelle i fließen
Referenzen
Jenson, S. K. und Domingue, J. O. 1988. "Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis." Photogrammetric Engineering and Remote Sensing 54 (11): 1593–1600.
Qin, C., Zhu, A. X., Pei, T., Li, B., Zhou, C., und Yang, L. 2007. "An adaptive approach to selecting a flow partition exponent for a multiple flow direction algorithm." International Journal of Geographical Information Science 21(4): 443-458.