Fonctionnement de l'outil Dériver le flux continu

Available with Image Server

Pour de nombreuses applications, il est primordial de bien comprendre la manière dont l'eau s'écoule dans le paysage une fois qu'elle est tombée sous forme de précipitation. Les modèles numériques de terrain (MNT) constituent le jeu de données fondamental de la modélisation du flux en surface. Toutefois, ces données ne sont pas une réprésentation parfaite (il existe souvent de petites erreurs d'altitude ou des représentations erronées des entités de paysage).

Vous devez donc prétraiter le MNT en entrée avant de déterminer la direction de l'écoulement d'eau. Le conditionnement hydrologique fait référence à la modification des valeurs d'altitude du MNT en entrée de sorte que l'écoulement en surface soit continu, tout comme le véritable écoulement en surface. Le conditionnement hydrologique est nécessaire pour traiter les instances dans lesquelles les limitations du MNT perturbent le résau d'écoulement (par exemple, une altitude fausse peut agir comme des cuvettes qui accumulent artificiellement le flux et l'arrêtent), ce qui empêche de déterminer la direction du flux à l'extérieur des cellules des cuvettes. Les ponts, barrages et caniveaux qui ne sont pas inclus dans le modèle de surface peuvent également créer des sorties de direction de flux et d'accumulation de flux erronées.

L’outil Dériver le flux continu résout les sorties de direction et d’accumulation de flux erronées, non pas en modifiant les données MNE en entrée, mais en appliquant l’algorithme du chemin de moindre coût. L'algorithme du chemin de moindre coût implique une minimisation du dénivelé positif sur le raster de surface en entrée. En d'autres termes, cellule par cellule, une étape d'optimisation est requise pour identifier le voisin en amont minimum. Par ailleurs, des règles spéciales pour les cellules de cuvettes et les cellules NoData sont également appliquées. Les cellules de cuvettes ou de dépressions peuvent correspondre à des cellules individuelles ou à un groupe de cellules dont les voisins possèdent une valeur d'altitude plus élevée que celle de la cellule ou du groupe de cellules traité. Les cellules NoData sont considérées comme des emplacements où les informations sont inconnues et ne sont pas utilisées dans le traitement.

Cet outil utilise une surface MNT comme entrée et crée un raster indiquant la direction et l'accumulation du flux au niveau de chaque cellule.

Si le raster de surface en entrée contient de véritables cuvettes ou zones de dépression, ces dernières doivent être spécifiées à l'aide du paramètre Données raster ou d’entités de dépression en entrée. Si un jeu de données raster est spécifié, les cellules du raster en entrée qui contiennent des données sont considérées comme des cellules de dépressions valides. Si un jeu de classes d'entités est spécifié, les entités sont rastérisées dans la même résolution que les données de surface en entrée et le raster résultant est utilisé pour spécifier les cellules de dépressions valides.

L’outil fournit deux méthodes pour déterminer la direction de flux à l’aide du paramètre Type de direction de flux : la méthode D8 modélise la direction du flux de chaque cellule vers son voisin en aval le plus abrupt et est limitée à une seule direction (Jenson et Domingue, 1988). La méthode MFD (Multiple Flow Direction) permet de partitionner le flux entre tous les voisins en aval à l'aide d'une approche qui adapte l'exposant de partitionnement du flux en fonction des conditions de terrain locales (Qin et al., 2007).

Si Raster de pondération d’accumulation en entrée est spécifié, une pondération est appliquée à chaque cellule lors de la dérivation de l'accumulation.

Calculer la direction de flux et l’accumulation de flux

Dans l'algorithme Dériver le flux continu, deux étapes de base de l'approche du chemin de moindre coût sont appliquées au calcul de l'itinéraire du flux. Tout d'abord, les sorties valides sont définies. Les sorties valides sont les cellules dans lesquelles de l'eau peut se déverser mais ne peut pas en sortir. Par défaut, les cellules des sorties sont celles qui se trouvent au bord du raster de surface en entrée. Si le paramètre Données raster ou d’entités de dépression en entrée est spécifié, les cellules du raster en entrée ou du jeu de classes d'entités sont également marquées comme des sorties valides depuis le début de l'algorithme. La deuxième étape consiste à parcourir le raster de surface en entrée et à dériver la direction du flux et l'accumulation du flux au niveau de chaque cellule en traitant les cellules dans l'ordre, de l'altitude la plus basse à l'altitude la plus élevée. Ces deux principes permettent un déplacement de la cellule actuelle vers la prochaine cellule plus élevée dans la direction de la pente ascendante la moins raide (Metz et al., 2011; Ehlschlaeger, 1989).

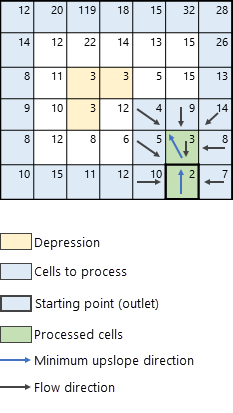
Le diagramme ci-après illustre la logique générale suivie. Les cas spéciaux, tels que les cellules de dépressions (cuvettes) non spécifiées explicitement comme des dépressions via le paramètre Données raster ou d’entités de dépression en entrée et les cellules NoData sont expliqués respectivement dans les sections Traiter les cellules de dépressions inconnues et Cellules NoData dans le raster de surface en entrée.

Figure 1. L'algorithme du chemin de moindre coût permettant de déterminer le calcul de l'itinéraire du flux et l'accumulation du flux, conformément à Metz et al., 2011; Ehlschlaeger, 1989, est illustré.

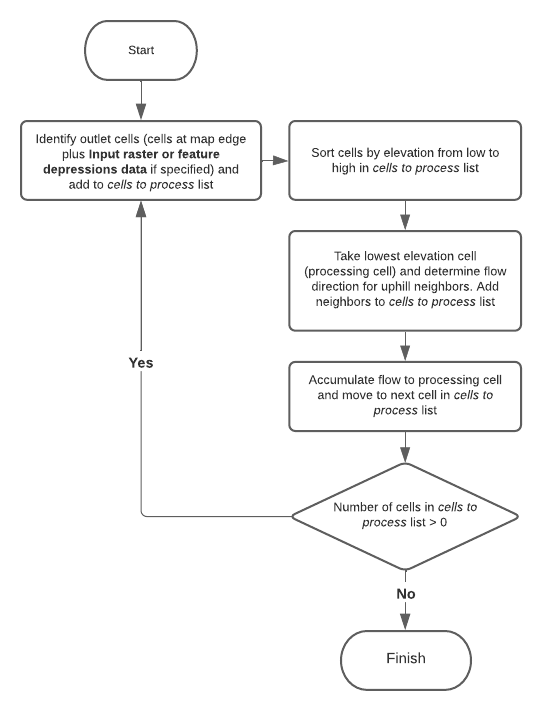
Logique de l'outil Dériver le flux continu

Dans cette section, vous allez parcourir un exemple de traitement des données d'altitude et de détermination de la direction du flux et de l'accumulation du flux cellule par cellule par l'outil Dériver le flux continu. Cet exemple illustre le traitement en présence d'une dépression non incluse dans le paramètre facultatif Données raster ou d’entités de dépression en entrée (voir Figure 2).

Figure 2. Un exemple de données d'altitudes synthétiques avec une taille de cellule de 1 est illustré. Cet exemple comporte une dépression autour de la zone du milieu du raster de surface, indiquée en jaune, qui n'a pas été spécifiée dans le paramètre Données raster ou d’entités de dépression en entrée.

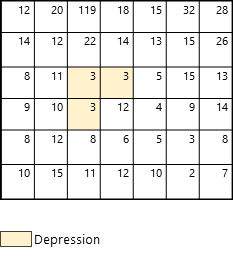
Tout d'abord, les sorties sont identifiées. Elles correspondent aux cellules au bord de la carte (en bleu dans la Figure 3).

Figure 3. Les cellules candidates des sorties identifiées comme sorties potentielles à l'étape 1 sont indiquées.

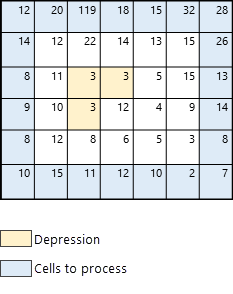
Une fois que les cellules des sorties ont été identifiées (cellules en bleu), l'algorithme recherche la cellule dont l'altitude est la plus basse, à partir de laquelle la recherche doit commencer. Dans cet exemple, la cellule la plus basse (altitude 2) est mise en évidence avec une bordure noire épaisse dans la Figure 4.

Figure 4. À l'étape 2, le point de départ est identifié en triant les cellules des sorties potentielles par altitude et en choisissant celle dont l'altitude est la plus faible, mise en évidence avec une bordure noire épaisse.

La prochaine étape consiste à identifier les voisins de la cellule de traitement (en vert) dont la valeur d'altitude est supérieure à celle de la cellule de traitement. Ces voisins sont ajoutés aux cellules possibles pouvant être traités ensuite, indiquées dans la Figure 5. La prochaine cellule à traiter est déterminée en recherchant le voisin en amont dont l'altitude est la plus basse (dans notre exemple, il s'agit de la cellule dont la valeur d'altitude est 3) qui correspond à la direction en amont minimum (flèche bleue dans la Figure 5). La direction et l'accumulation du flux des cellules en amont voisines sont calculées de manière séquentielle pour la cellule de traitement. La direction du flux est déterminée à l'aide de la méthode spécifiée dans le paramètre Type de direction de flux. Deux méthodes permettent de déterminer la direction du flux : D8 et MFD. Pour une explication de ces deux méthodes, reportez-vous à la section Méthodes de détermination de la direction du flux ci-après.

Figure 5. À l'étape 3, les cellules voisines de la cellule de traitement actuelle ont été identifiées. Les cellules mises en évidence en bleu sont celles qui peuvent potentiellement être traitées ensuite. Les flèches noires correspondent à la direction du flux et les flèches bleues, au chemin à suivre pour le traitement.

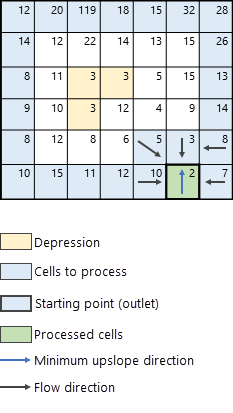
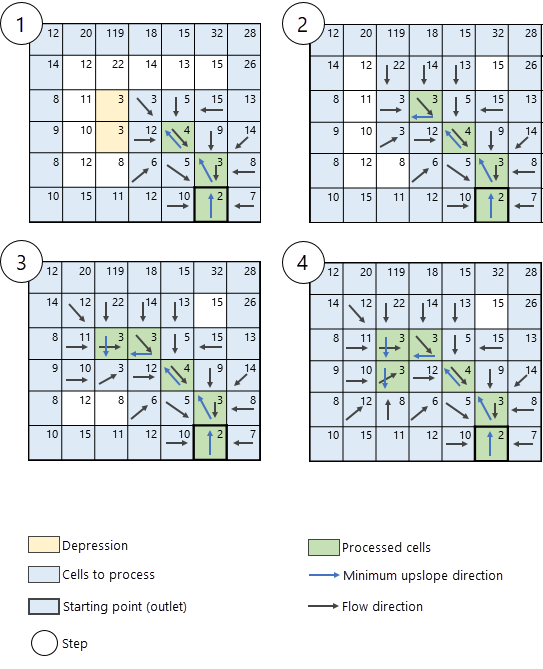
L'algorithme continue de la même manière, en identifiant les cellules voisines de la cellule de traitement actuelle dans la direction de la pente ascendante minimum. L’itération suivante de l'algorithme est illustrée dans la Figure 6.

Figure 6. L’itération suivante est illustrée. Comme dans la Figure 5, les cellules mises en évidence en bleu sont celles qui peuvent potentiellement être traitées ensuite. La prochaine cellule à traiter dans ce diagramme est la cellule 3, en vert. Les flèches noires correspondent à la direction du flux et les flèches bleues, à la direction du chemin de moindre coût.

Traiter les cellules de dépressions inconnues

Les cellules de dépressions (ou cuvettes) peuvent correspondre à des cellules individuelles ou à un groupe de cellules dont les voisins possèdent une valeur d'altitude plus élevée que celle de la cellule ou du groupe de cellules de traitement. Si elles ne sont pas incluses dans le paramètre Données raster ou d’entités de dépression en entrée, elles sont considérées comme des cellules de dépressions par l'outil. Dans ce scénario, si une cellule ou un groupe de cellules de dépressions inconnu est rencontré, le chemin suit la descente la plus abrupte (et non la cellule voisine en amont la plus basse) jusqu'à ce qu'il atteigne le fond de la dépression, en définissant la direction et l'accumulation du flux le long du chemin de la dépression. Ce traitement est illustré à la Figure 7.

Figure 7. La séquence de traitement de chaque cellule à l'intérieur de la dépression, de gauche à droite, est illustrée. La direction et l'accumulation du flux sont déterminées à mesure du traitement de chaque cellule à l'intérieur de la dépression. Le traitement dans la dépression s'effectue dans le sens de la descente la plus abrupte et non en suivant la cellule voisine en amont la plus basse.

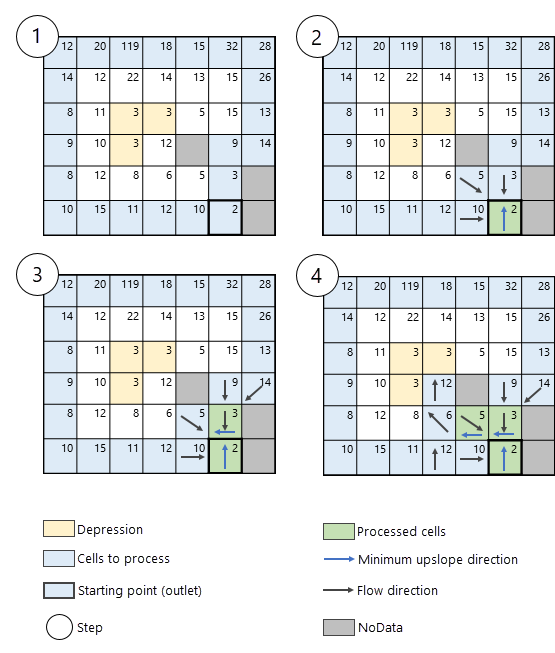
Cellules NoData dans le raster de surface en entrée

Les cellules NoData dans le raster de surface en entrée sont celles dont la valeur n'est pas connue. Ces cellules peuvent exister dans le raster de surface et être rencontrées lors de l'algorithme Dériver le flux continu. Si c'est le cas, elles ne sont pas traitées et l'algorithme les contourne, comme illustré dans la Figure 8.

Figure 8. Les cellules NoData à l'intérieur du raster de surface en entrée sont ignorées par l'outil Dériver le flux continu. Les cellules NoData extérieures repoussent les limites du raster de surface en entrée vers les voisins possédant des valeurs de données valides. Les dernières étapes des calculs permettant de déterminer la direction et l'accumulation du flux sont identiques.

Méthodes de détermination de la direction du flux

Dans la méthode D8, vous pouvez calculer la direction d’un flux en recherchant la direction de la descente la plus raide ou la pente maximale de chaque cellule (Jenson et Domingue, 1988). Elle est calculée comme suit :

pente_maximale = changement_de_valeur-z/distance

La distance est calculée entre les centres des cellules. Pour les cellules proches du coin, l’algorithme vérifie que la pente maximale vers la cellule de traitement sélectionnée est égale au maximum ; sinon, la direction de flux sera définie vers la cellule avec la pente maximale de la cellule proche du coin indiquée. Si la valeur z d’une cellule présente le même changement dans plusieurs directions, la direction de flux D8 est ambigüe et la valeur sera la somme des directions possibles.

Lorsque la direction de descente la plus raide est trouvée, la cellule en sortie est codée avec la valeur représentant cette direction.

Dans la méthode MFD, le flux est partitionné sur tous les voisins descendants (Qin et al., 2007). La quantité de flux reçue par chaque voisin descendant est estimée sous forme de gradient de pente maximum, qui autorise les conditions du terrain local. L’expression pour estimer le flux MFD se présente comme suit :

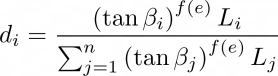
Où :

• d_i = Portion de flux à partir de chaque cellule qui s’écoule dans la cellule i
• f (e) = Exposant qui s’adapte aux conditions du terrain local et est fourni par

  

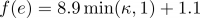
• β = Angle de la pente descendante (en radians)
• n = nombre de cellules qui s’écoulent dans la cellule i
• L_i, L_j = Facteur ajusté qui représente la distance entre la cellule de traitement et les cellules orthogonales et diagonales
• κ = Pente maximale sur les cellules qui s’écoulent dans la cellule i

Une fois que la direction et l'accumulation du flux ont été déterminées, ainsi que la direction du chemin de moindre coût, la cellule de traitement est marquée comme traitée et la prochaine cellule de la file d'attente est analysée. L'algorithme procède de cette manière jusqu'à ce que toutes les cellules du raster de surface en entrée aient été traitées. En d'autres termes, la direction du flux et l'accumulation de flux ont été déterminées pour toutes les cellules.

Bibliographie

Ehlschlaeger, C. R. 1989. « Using the AT Search Algorithm to Develop Hydrologic Models from Digital Elevation Data. » International Geographic Information Systems (IGIS) Symposium 89: 275-281.

Jenson, S. K., and Domingue, J. O. 1988. « Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis. » Photogrammetric Engineering and Remote Sensing 54 (11): 1593–1600.

Metz, M., Mitasova, H., & Harmon, R. S. 2011. « Efficient extraction of drainage networks from massive, radar-based elevation models with least cost path search. » Hydrology and Earth System Sciences 15(2): 667-678.

Qin, C., Zhu, A. X., Pei, T., Li, B., Zhou, C., & Yang, L. 2007. « An adaptive approach to selecting a flow partition exponent for a multiple flow direction algorithm. » International Journal of Geographical Information Science 21(4): 443-458.